SEm/labore/02 interpolation
(→Sägezahn) |
|||
| (15 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{TOC right}} | {{TOC right}} | ||
| − | = | + | = Funktionsgenerator mit Interpolationsberechnung = |
| − | + | ||
| − | + | ||
| − | + | == Einleitung == | |
| − | + | In diesem Labor werden wir verschiedene Operationen mit Zahlen durchführen. | |
| + | Dies am Beispiel der Interpolation der Punkte der Sinuskurve eines digitales Funktionsgenerator. | ||
| − | + | Die Berechnung der Interpolation basiert auf der Annäherung der Funktion zwischen 2 Punkten mit Polynomialfunktionen dritter Ordnung. | |
| + | Diese Methode gehört zur grossen Familie der ''Splines''. | ||
| − | + | Die Schaltung befindet sich in der Library '''SineInterpolator''', die Testbank in der Library '''SineInterpolator_test'''. | |
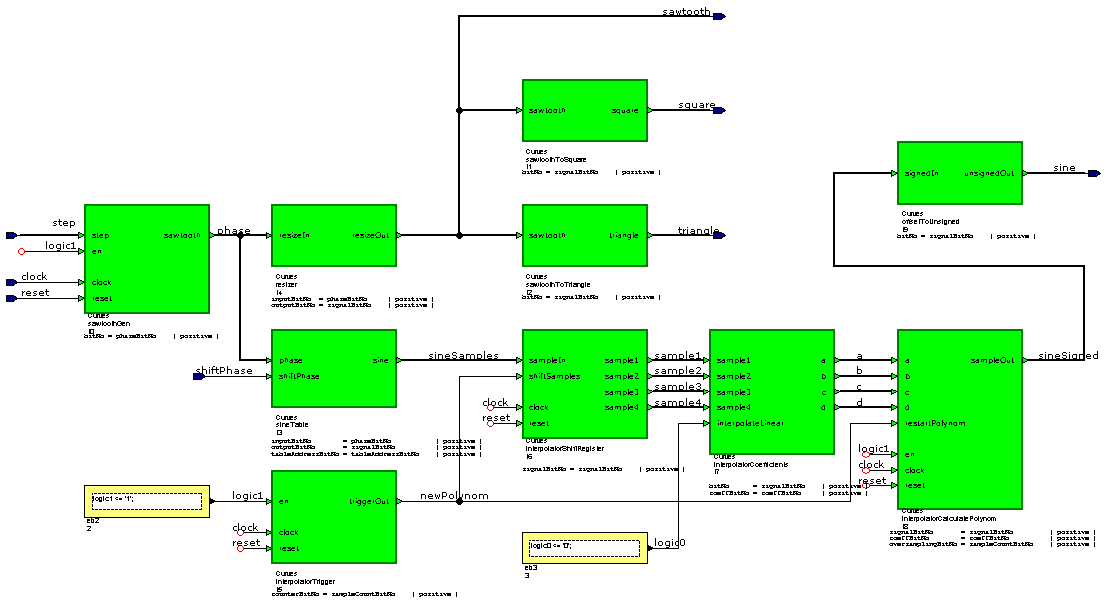
| − | + | [[Image:SEm_sineGen.png|center|Funktionsgenerator mit Berechnung des Sinus durch Interpolation]] | |
| − | + | == Sägezahn == | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | In dieser Schaltung ist die Anzahl Bits der Phase nicht gleich derjenigen der Funktionsgenerator-Ausgänge. | |
| − | + | Wenn Ihr die Basisausgänge ''Sägezahn'', ''Viereck'' und ''Dreieck'' erstellt, ändert der Block '''resizer''' die Anzahl Bits des Phasensignals und passt es den Ausgängssignalen an. Dabei gibt es drei Fälle zu beachten: | |
| − | + | * Die Anzahl Bits der Ausgänge ist kleiner als die des Phasensignals: in diesem Fall werden die MSBs behalten. | |
| + | * Die Anzahl Bits der Ausgänge ist gleich wie die des Phasensignals: in diesem Fall werden alle Bits übertragen. | ||
| + | * Die Anzahl Bits der Ausgänge ist grösser als die des Phasensignals: in diesem Fall wird die MSBs des Phasensignals ins Sägezahnsignal gelegt. | ||
| − | + | === VHDL Code === | |
| − | + | {{TaskBox|content= | |
| + | Mit Hilfe des Konstruktes '''if ... generate''', schreiben Sie den VHDL Code des '''resizer'''-Blocks.}} | ||
| − | + | === Simulation === | |
| + | |||
| + | {{TaskBox|content= | ||
| + | Kompilieren und simulieren Sie den Block '''sineGen_tb'''. | ||
| + | Ändern Sie die Anzahl Bits des Phasensignals und überprüfen Sie die Anpassung der Anzahl Bits in jedem möglichen Operationsfall.}} | ||
| + | |||
| + | == Sinustabelle == | ||
| + | |||
| + | [[Image:SEm_sineTable.png|thumb|Sinustabelle]] | ||
| + | |||
| + | Die Interpolation wird durchgeführt abhand einer Tabelle, welche 8 Werte der Sinusfunktion im ersten Viertel der Periode enthält. Um die Werte für die ganze Periode | ||
| + | anzuwenden, wird das Sägezahnsignal des Phasenzählers wie folgt angewandt: | ||
| + | |||
| + | * Der MSB gibt an, ob das Vorzeichen zu ändern ist. | ||
| + | * Der nächste Bit meldet, dass die Phase geändert sein soll, um die Tabelle in der umgekehrten Richtung zu lesen, dies für den zweiten und den vierten Viertel der Periode. | ||
| + | * Die 3 weitere Bits ('''tableAddressBitNb = 3''') sind als Adresse für das Lesen der Tabellenwerte angewandt. | ||
| + | * Alle andere Bits werden vernachlässigt. | ||
| + | |||
| + | === VHDL Code === | ||
| + | |||
| + | {{TaskBox|content= | ||
| + | Schreiben Sie die VHDL Architektur des Sinuswellengenerators.}} | ||
| + | |||
| + | Die Adresse der tabelle stammt aus den 3 Bits nach den 2 MSBs. Sie zählt die Sequenz 0, 1, 2, 3, 4, 5, 6, 7, 0, 7, 6, 5, 4, 3, 2, 1, 0, 1, 2, 3, .... | ||
| + | |||
| + | Die Sinustabelle enthält die Hexadezimalwerte 0000 oder 7FFF (abhängig vom zweithöchstwertigsten Bit), 18F9, 30FB, 471C, 5A82, 6A6D, 7641 und 7D89. | ||
| + | |||
| + | Wenn das MSB der Phase gleich '1' ist, so wird das Vorzeichen des Tabellenwertes invertiert, um den Ausgang zu erzeugen. | ||
=== Simulation === | === Simulation === | ||
| − | + | {{TaskBox|content= | |
| + | Kompilieren Sie und simulieren Sie den Block '''sineGen_tb'''. Prüfen Sie die Funktionalität des Sinuswellensignalgenerators.}} | ||
== Interpolation == | == Interpolation == | ||
| − | + | Die Interpolation wird gemacht, indem man eine verschiedene Polynomialfunktion 3. Ordnung zu jedem Intervall zwischen zwei Punkte der Sinustabelle zuweist: | |
| − | ''' y = a·k | + | ''' y = a·k<sup>3</sup> + b·k<sup>2</sup> + c·k +d ''' |
| − | + | Während dieser Berechnung wird der jeweilige Punkt der Tabelle mit '''k = 0''' definiert, der vorige Punkt mit '''k = -1''' und der nächste mit '''k = 1''' definiert. Wir werden die Polynomialfunktion für '''n = 2<sup>m</sup>''' Punkte zwischen 0 und 1 berechnen. | |
| − | + | Um die Kontinuität der Kurve beim Übergang vom Polynom des Segments '''-1 < k < 0''' und dem von '''0 < k < 1''', spezifieren wir, dass die derivative am Punkt '''y(k=0)''' gleich der Steigung zwischen den Punkten '''y(k=-1)''' und '''y(k=1)'''sein soll. Wir werden dasselbe für alle Punkte der zu interpolierenden Funktion machen. | |
| − | + | Das Segment '''0 < k < 1''' dient somit den 4 folgenden Bedingungen: | |
| − | ''' y(k=0) = y0''': | + | ''' y(k=0) = y0''': das Polynom geht durch den Punkt '''(k=0, y=y0)''', |
| − | ''' y(k=1) = y1''': | + | ''' y(k=1) = y1''': das Polynom geht durch den Punkt '''(k=1, y=y1)''', |
| − | ''' y'(k=0) = [y(k=1) - y(k=-1)] / 2''': | + | ''' y'(k=0) = [y(k=1) - y(k=-1)] / 2''': die Ableitung am Punkt '''(k=0)''' ist die Steigung zwischen '''y(k=-1)''' und '''y(k=1)''', |
| − | ''' y'(k=1) = [y(k=2) - y(k=0)] / 2''': | + | ''' y'(k=1) = [y(k=2) - y(k=0)] / 2''': die Ableitung am Punkt '''(k=1)''' ist die Steigung zwischen '''y(k=0)''' und '''y(k=2)'''. |
| − | + | Diese 4 Bedingungen dienen zur Bestimmung der 4 Koeffizienten '''a''', '''b''', '''c''' und '''d''' des Polynoms anhand der 4 Punkte '''y(k=-1)''' bis '''y(k=2)''' der zu interpolierenden | |
| + | Kurve. Die Auflösung dieses Gleichungssystems gibt uns die folgenden Werte der Koeffizienten: | ||
''' a = 1/2 [ - y(k=-1) +3·y(k=0) -3·y(k=1) + y(k=2) ]''' | ''' a = 1/2 [ - y(k=-1) +3·y(k=0) -3·y(k=1) + y(k=2) ]''' | ||
| Line 66: | Line 95: | ||
''' d = y(k=0)''' | ''' d = y(k=0)''' | ||
| − | + | Um die Berechnungen zu vereinfachen werden wir den doppelten Wert der Koeffizienten evaluieren und später die berechnete Werte des Polynoms durch 2 teilen. | |
| − | + | Beim Auftreten jedes neuen Werts des ursprünglichen Signals (hier die Sinustabelle), müssen die Polynomkoeffiziente neu berechnet werden. Dann, in der Zwischenzeit, wird die Polynomilafunktion berechnet, um den jeweilgen Wert des Ausgangssignal zu bestimmen. | |
| − | === | + | === Generator von Sequenzierungsimpulsen === |
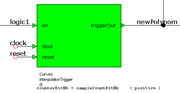
| − | + | [[Image:SEm_interpolatorTrigger.png|thumb|Genrator von Sequenzierungsimpulsen]] | |
| − | + | {{TaskBox|content= | |
| + | Schreiben Sie die VHDL Architektur des Generators von Sequenzierungsimpulsen.}} | ||
| − | + | Diese Schaltung ermittelt einen Impuls mit der Dauer einer Taktperiode bei jedem Polynomwechsel, das heisst zu jedem neuen Kurvensegment. | |
| − | + | Dies erfolgt zu jeden '''2<sup>n</sup>''' Taktperioden wo '''en = '1'''', wobei '''n = sampleCountBitNb = phaseBitNb-2-tableAddressBitNb'''. In unserem Laborbeispiel sind '''phaseBitNb = 10''' und '''sampleCountBitNb = 5'''. | |
| − | === | + | === Schieberegister === |
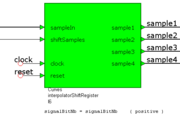
| − | + | [[Image:SEm_interpolatorShiftRegister.png|thumb|Schieberegister]] | |
| − | + | {{TaskBox|content= | |
| + | Schreiben Sie die VHDL Architektur des Schieberegisters, welcher die 4 letzten Punkte der zu interpolendierenden Funktion speichert.}} | ||
| − | + | Bei jedem Synchronisationsimplus '''shiftSamples''' speichert dis Schaltung den neuen Wert der zu interpolendierenden Funktion, '''sampleIn''', und speichert es als letzes Abtastwert, '''sample4'''. Zugleich schiebt er den gespeicherten Wert von '''sample4''' zurück in '''sample3''', usw... | |
| − | = | + | {{WarningBox|content=Verwenden Sie ein Array von Zahlen, um den Shieberegister zu beschreiben.}} |
| − | + | === Berechnung der Koeffizienten === | |
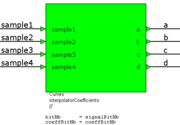
| − | [[Image:SEm_interpolatorCoefficients.png|thumb| | + | [[Image:SEm_interpolatorCoefficients.png|thumb|Block zur Berechnung der Koeffizienten für die Interpolation]] |
| − | + | {{TaskBox|content= | |
| + | Öffnen Sie die Library '''ieee.numeric_std''' und durchsuchen Sie die Auswirkung der Multiplikation eines Signals von Typ '''signed''' durch eine ganze Zahl. Prüfen Sie ebenfalls das Funktionieren der Funktion '''resize'''. Sie ist hier sehr nützlich, um die Anzahl der Bits der Signale zu bestimmen.}} | ||
| + | |||
| + | Die Koeffizienten werden wie folgt berechnet: | ||
''' a = - sample1 +3·sample2 -3·sample3 + sample4''' | ''' a = - sample1 +3·sample2 -3·sample3 + sample4''' | ||
| Line 104: | Line 138: | ||
''' d = sample2''' | ''' d = sample2''' | ||
| − | + | {{TaskBox|content= | |
| + | Schreiben Sie die VHDL Architektur des Blocks, welcher die Koeffizienten des Polynoms als Funktion der 4 letzten Punkten der zu interpolendierenden Funktion berechnet.}} | ||
| − | + | [[File:SEm_sinegen_coeffs.svg|thumb|Interpolationskoeffizienten]] | |
| + | Die von Ihnen berechneten Koeffizienten können mit der [[Media:SEm_sinegen_coeffs.svg|nebenstehenden Waveform]] überprüft werden. | ||
| − | == | + | {{TaskBox|content= |
| + | Erklären Sie die getroffene Wahl im Schema '''coeffBitNb := signalBitNb+4'''.}} | ||
| − | + | === Berechnung des Polynoms === | |
| − | [[Image:SEm_interpolatorPolynom.png|thumb| | + | [[Image:SEm_interpolatorPolynom.png|thumb|Block zur Berechnung der Interpolation]] |
| − | + | {{TaskBox|content= | |
| + | Schreiben Sie die VHDL Architektur des Blocks, welcher den Wert des Interpolationspolynom bei jeder neuen Taktperiode berechnet.}} | ||
| − | + | Das Polynom wird iterativ berechnet. | |
| − | + | Als Beispiel, für eine Funktion 1. Ordnung, '''y(x) = a·x + b''', ist der nächste Wert gleich '''y(x+eps) = y(x) + a·eps'''. Die berechnet sich, indem anfangs '''u = a·eps''', '''y(0) = b''' initialisiert wird, und indem '''y(i+1) = y(i) + u''' bei jeder Taktperiode neu berchenet wird. | |
| − | + | Für eine Funktion 2. Ordnung, '''y(x) = a·x<sup>2</sup> + b·x + c''', ergibt sich '''y(x+eps) = y(x) + u(x)''', mit '''u(x) = 2·a·eps·x + (a·eps<sup>2</sup> + b·eps)'''. Der Zusatz '''u(x)''' berechnet sich mit der Methode, welche für eine Funktion 1. Ordnung vorgegeben wurde. Dies berechnet sich also mit '''v = 2·a·eps<sup>2</sup>''', '''u(0) = a·eps<sup>2</sup> + b·eps''', '''y(0) = c''' bei der Initialisation und mit '''y(i+1) = y(i) + u(i)''' und '''u(i+1) = u(i) + v''' bei jeder neuen Taktperiode. | |
| − | + | Die Berechnung der Funktion dritter Ordnung erfolgt ähnlich. | |
| − | + | Für die digitale Berechnung wird '''eps''' als gleich einer negativen Potenz von 2 gewählt, was es erlaubt, Werte durch eine Verschiebung zu berechnen. Ebenso, um mit ganzen Zahlen zu verbleiben, wird man die Funktion '''y(i)''' mit einer Potenz von 2 multipliziert berechnen, und eine Abschlussverschiebung wird uns den Abtastwert des Polynoms geben. | |
| − | + | Somit ist unser Algorithmus der folgende: | |
| − | + | ||
| − | + | * Bei der Ankunft eines neuen Abtastwertes werden die Initialwerte zur iterativen Bestimmung des Polynoms berechnet. | |
| + | * Zwischen zwei Abtastwerte wird die Berechnung der Polynomialfunktion mit Hilfe von Additionen durchgeführt, abhand der iterativen Gleichungen. | ||
| − | + | Die Initialwerte sind die folgende: | |
| − | ''' | + | ''' x = 2·d·2<sup>(3·m)</sup>''' |
| − | ''' v = 6·a + 2·b·2 | + | ''' u = a + b·2<sup>m</sup> + c·2<sup>(2·m)</sup>''' |
| + | |||
| + | ''' v = 6·a + 2·b·2<sup>m</sup>''' | ||
''' w = 6·a''' | ''' w = 6·a''' | ||
| Line 141: | Line 181: | ||
''' y = d''' | ''' y = d''' | ||
| − | + | Die Iterativberechnung des Polynoms wird wie folgt durchgeführt: | |
''' x = x + u''' | ''' x = x + u''' | ||
| Line 149: | Line 189: | ||
''' v = v + w''' | ''' v = v + w''' | ||
| − | ''' y = x / 2·2 | + | ''' y = x / (2·2<sup>(3·m)</sup>)''' |
| − | + | Es ist offensichtlich, dass, wegen der Verschiebungen '''2<sup>m</sup>''', die Anzahl der Bits der internen Signale höher sein muss als die Anzahl der Bits der Eingangs- oder Ausgangswerte. Schätzen Sie die notwendige Grösse für diese Signale als Funktion der Verschiebung '''m = oversamplingBitNb'''. Geben Sie diesen Signalen 8 zusätzliche Bits, um sicherzustellen, dass kein Overflow auftreten wird. | |
| − | + | Wiederum wird die Funktion '''resize''' hier von grossem Nutzen sein. | |
=== Simulation === | === Simulation === | ||
| − | + | {{TaskBox|content= | |
| − | + | Kompilieren Sie und simulieren Sie den Block '''sineGen_tb''' neu. Prüfen Sie die Form des Sinuswelle nach Interpolation.}} | |
| − | + | ||
| + | {{TaskBox|content= | ||
| + | Verkleinern Sie die Anzahl Bits der Signale in der Schaltung überall, wo es möglich ist, unter Beibehaltung der selben Sinuswelle nach Interpolation.}} | ||
| − | {{navNamed|left=SEm/ | + | {{navNamed|left=SEm/labore/01_generator|left_name=01 Funktionsgenerator|up=SEm/labore|up_name=Anleitung auf Deutsch|right=SEm/labore/03_konverter|right_name=03 Digital / Analog Wandler}} |
| − | [[Category:SEm]] | + | [[Category:Bachelor]][[Category:SEm]][[Category:Deutsch]] |
Latest revision as of 14:37, 8 February 2021
|
Funktionsgenerator mit Interpolationsberechnung
Einleitung
In diesem Labor werden wir verschiedene Operationen mit Zahlen durchführen. Dies am Beispiel der Interpolation der Punkte der Sinuskurve eines digitales Funktionsgenerator.
Die Berechnung der Interpolation basiert auf der Annäherung der Funktion zwischen 2 Punkten mit Polynomialfunktionen dritter Ordnung. Diese Methode gehört zur grossen Familie der Splines.
Die Schaltung befindet sich in der Library SineInterpolator, die Testbank in der Library SineInterpolator_test.
Sägezahn
In dieser Schaltung ist die Anzahl Bits der Phase nicht gleich derjenigen der Funktionsgenerator-Ausgänge.
Wenn Ihr die Basisausgänge Sägezahn, Viereck und Dreieck erstellt, ändert der Block resizer die Anzahl Bits des Phasensignals und passt es den Ausgängssignalen an. Dabei gibt es drei Fälle zu beachten:
- Die Anzahl Bits der Ausgänge ist kleiner als die des Phasensignals: in diesem Fall werden die MSBs behalten.
- Die Anzahl Bits der Ausgänge ist gleich wie die des Phasensignals: in diesem Fall werden alle Bits übertragen.
- Die Anzahl Bits der Ausgänge ist grösser als die des Phasensignals: in diesem Fall wird die MSBs des Phasensignals ins Sägezahnsignal gelegt.
VHDL Code
Simulation
Sinustabelle
Die Interpolation wird durchgeführt abhand einer Tabelle, welche 8 Werte der Sinusfunktion im ersten Viertel der Periode enthält. Um die Werte für die ganze Periode anzuwenden, wird das Sägezahnsignal des Phasenzählers wie folgt angewandt:
- Der MSB gibt an, ob das Vorzeichen zu ändern ist.
- Der nächste Bit meldet, dass die Phase geändert sein soll, um die Tabelle in der umgekehrten Richtung zu lesen, dies für den zweiten und den vierten Viertel der Periode.
- Die 3 weitere Bits (tableAddressBitNb = 3) sind als Adresse für das Lesen der Tabellenwerte angewandt.
- Alle andere Bits werden vernachlässigt.
VHDL Code
Die Adresse der tabelle stammt aus den 3 Bits nach den 2 MSBs. Sie zählt die Sequenz 0, 1, 2, 3, 4, 5, 6, 7, 0, 7, 6, 5, 4, 3, 2, 1, 0, 1, 2, 3, ....
Die Sinustabelle enthält die Hexadezimalwerte 0000 oder 7FFF (abhängig vom zweithöchstwertigsten Bit), 18F9, 30FB, 471C, 5A82, 6A6D, 7641 und 7D89.
Wenn das MSB der Phase gleich '1' ist, so wird das Vorzeichen des Tabellenwertes invertiert, um den Ausgang zu erzeugen.
Simulation
Interpolation
Die Interpolation wird gemacht, indem man eine verschiedene Polynomialfunktion 3. Ordnung zu jedem Intervall zwischen zwei Punkte der Sinustabelle zuweist:
y = a·k3 + b·k2 + c·k +d
Während dieser Berechnung wird der jeweilige Punkt der Tabelle mit k = 0 definiert, der vorige Punkt mit k = -1 und der nächste mit k = 1 definiert. Wir werden die Polynomialfunktion für n = 2m Punkte zwischen 0 und 1 berechnen.
Um die Kontinuität der Kurve beim Übergang vom Polynom des Segments -1 < k < 0 und dem von 0 < k < 1, spezifieren wir, dass die derivative am Punkt y(k=0) gleich der Steigung zwischen den Punkten y(k=-1) und y(k=1)sein soll. Wir werden dasselbe für alle Punkte der zu interpolierenden Funktion machen.
Das Segment 0 < k < 1 dient somit den 4 folgenden Bedingungen:
y(k=0) = y0: das Polynom geht durch den Punkt (k=0, y=y0),
y(k=1) = y1: das Polynom geht durch den Punkt (k=1, y=y1),
y'(k=0) = [y(k=1) - y(k=-1)] / 2: die Ableitung am Punkt (k=0) ist die Steigung zwischen y(k=-1) und y(k=1),
y'(k=1) = [y(k=2) - y(k=0)] / 2: die Ableitung am Punkt (k=1) ist die Steigung zwischen y(k=0) und y(k=2).
Diese 4 Bedingungen dienen zur Bestimmung der 4 Koeffizienten a, b, c und d des Polynoms anhand der 4 Punkte y(k=-1) bis y(k=2) der zu interpolierenden Kurve. Die Auflösung dieses Gleichungssystems gibt uns die folgenden Werte der Koeffizienten:
a = 1/2 [ - y(k=-1) +3·y(k=0) -3·y(k=1) + y(k=2) ]
b = 1/2 [ 2·y(k=-1) -5·y(k=0) +4·y(k=1) - y(k=2) ]
c = 1/2 [ - y(k=-1) + y(k=1) ]
d = y(k=0)
Um die Berechnungen zu vereinfachen werden wir den doppelten Wert der Koeffizienten evaluieren und später die berechnete Werte des Polynoms durch 2 teilen.
Beim Auftreten jedes neuen Werts des ursprünglichen Signals (hier die Sinustabelle), müssen die Polynomkoeffiziente neu berechnet werden. Dann, in der Zwischenzeit, wird die Polynomilafunktion berechnet, um den jeweilgen Wert des Ausgangssignal zu bestimmen.
Generator von Sequenzierungsimpulsen
Diese Schaltung ermittelt einen Impuls mit der Dauer einer Taktperiode bei jedem Polynomwechsel, das heisst zu jedem neuen Kurvensegment.
Dies erfolgt zu jeden 2n Taktperioden wo en = '1', wobei n = sampleCountBitNb = phaseBitNb-2-tableAddressBitNb. In unserem Laborbeispiel sind phaseBitNb = 10 und sampleCountBitNb = 5.
Schieberegister
Bei jedem Synchronisationsimplus shiftSamples speichert dis Schaltung den neuen Wert der zu interpolendierenden Funktion, sampleIn, und speichert es als letzes Abtastwert, sample4. Zugleich schiebt er den gespeicherten Wert von sample4 zurück in sample3, usw...
Berechnung der Koeffizienten
Die Koeffizienten werden wie folgt berechnet:
a = - sample1 +3·sample2 -3·sample3 + sample4
b = 2·sample1 -5·sample2 +4·sample3 - sample4
c = - sample1 + sample3
d = sample2
Die von Ihnen berechneten Koeffizienten können mit der nebenstehenden Waveform überprüft werden.
Berechnung des Polynoms
Das Polynom wird iterativ berechnet.
Als Beispiel, für eine Funktion 1. Ordnung, y(x) = a·x + b, ist der nächste Wert gleich y(x+eps) = y(x) + a·eps. Die berechnet sich, indem anfangs u = a·eps, y(0) = b initialisiert wird, und indem y(i+1) = y(i) + u bei jeder Taktperiode neu berchenet wird.
Für eine Funktion 2. Ordnung, y(x) = a·x2 + b·x + c, ergibt sich y(x+eps) = y(x) + u(x), mit u(x) = 2·a·eps·x + (a·eps2 + b·eps). Der Zusatz u(x) berechnet sich mit der Methode, welche für eine Funktion 1. Ordnung vorgegeben wurde. Dies berechnet sich also mit v = 2·a·eps2, u(0) = a·eps2 + b·eps, y(0) = c bei der Initialisation und mit y(i+1) = y(i) + u(i) und u(i+1) = u(i) + v bei jeder neuen Taktperiode.
Die Berechnung der Funktion dritter Ordnung erfolgt ähnlich.
Für die digitale Berechnung wird eps als gleich einer negativen Potenz von 2 gewählt, was es erlaubt, Werte durch eine Verschiebung zu berechnen. Ebenso, um mit ganzen Zahlen zu verbleiben, wird man die Funktion y(i) mit einer Potenz von 2 multipliziert berechnen, und eine Abschlussverschiebung wird uns den Abtastwert des Polynoms geben.
Somit ist unser Algorithmus der folgende:
- Bei der Ankunft eines neuen Abtastwertes werden die Initialwerte zur iterativen Bestimmung des Polynoms berechnet.
- Zwischen zwei Abtastwerte wird die Berechnung der Polynomialfunktion mit Hilfe von Additionen durchgeführt, abhand der iterativen Gleichungen.
Die Initialwerte sind die folgende:
x = 2·d·2(3·m)
u = a + b·2m + c·2(2·m)
v = 6·a + 2·b·2m
w = 6·a
y = d
Die Iterativberechnung des Polynoms wird wie folgt durchgeführt:
x = x + u
u = u + v
v = v + w
y = x / (2·2(3·m))
Es ist offensichtlich, dass, wegen der Verschiebungen 2m, die Anzahl der Bits der internen Signale höher sein muss als die Anzahl der Bits der Eingangs- oder Ausgangswerte. Schätzen Sie die notwendige Grösse für diese Signale als Funktion der Verschiebung m = oversamplingBitNb. Geben Sie diesen Signalen 8 zusätzliche Bits, um sicherzustellen, dass kein Overflow auftreten wird.
Wiederum wird die Funktion resize hier von grossem Nutzen sein.
Simulation
Navigation
![]() 01 Funktionsgenerator
01 Funktionsgenerator
![]() Anleitung auf Deutsch
03 Digital / Analog Wandler
Anleitung auf Deutsch
03 Digital / Analog Wandler ![]()