SEm/laboratoires/02 interpolation
|
Générateur de fonctions avec calcul d'interpolation
Introduction
Dans ce laboratoire, nous allons effectuer des opérations sur des nombres. Ceci sera illustré par le clacul de l'interpolation de points de la fonction sinus d'un générateur de fonctions numérique.
Le calcul de l'interpolation se base sur l'approximation de la fonction entre deux points donnés par des fonctions polynomiales du troisième ordre. Cette méthode appartient à la grande famille des "splines".
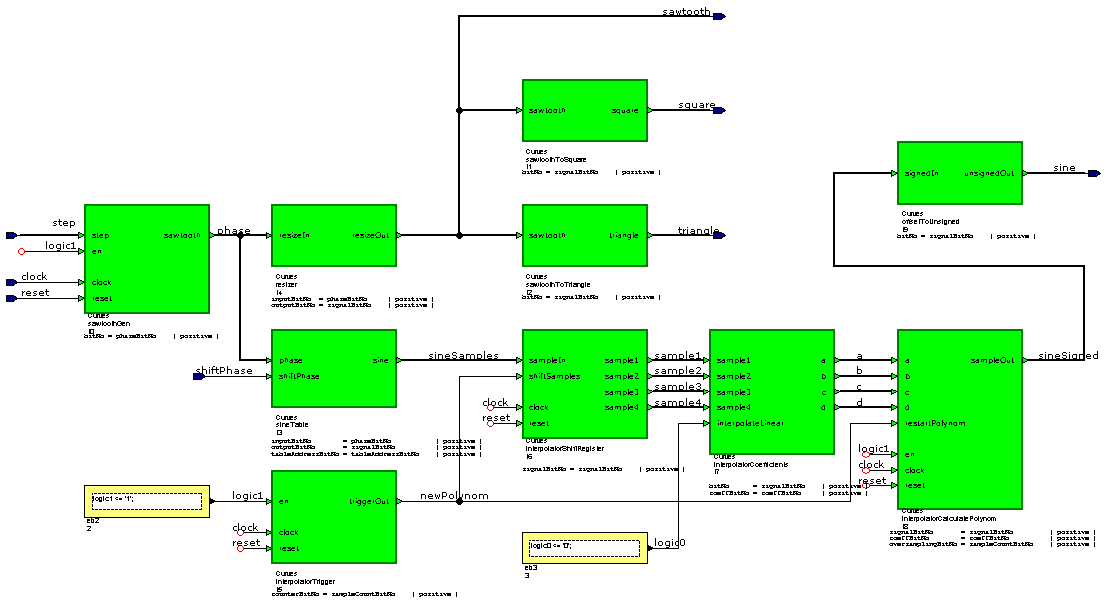
Le circuit se trouve dans la librairie SineInterpolator, le banc de test dans la librairie SineInterpolator_test.
Dent de scie
Dans ce circuit, le nombre de bits de la phase n'est pas identique à celui des sorties du générateur de fonctions.
Pour utiliser les blocs qui fournissent les signaux en dent de scie, triangulaire et carré, le bloc resizer modifie le nombre de bits du compteur de phase. 3 cas sont à prévoir:
- Le nombre de bits des sorties est supérieur à celui de la phase: il faut donc copier le signal de phase dans les bits de poids fort du signal en dent de scie
- Le nombre de bits des sorties est égal à celui de la phase: il suffit de copier le signal de phase dans celui en dent de scie
- Le nombre de bits des sorties est plus petit que celui de la phase: il faut ici conserver les bits de poids fort du signal de phase
VHDL Code
Simulation
Table de sinus
L'interpolation se fera à partir d'une table contenant 8 valeurs de sinus pour un quart de sa période. Pour fonctionner sur toute la période, le signal en dents de scie provenant du compteur et considéré comme phase du sinus est utilisé comme suit:
- Le bit de poids fort signale le changement de signe des valeurs du sinus.
- Le bit suivant signale un changement à apporter à la phase pour lire la table dans le sens inverse, ceci pour les deuxième et quatrième quarts de la période.
- Les 3 bits suivants (tableAddressBitNb = 3) sont utilisés pour adresser les valeurs de la table.
- Les autres bits sont ignorés.
Code VHDL
L'adresse de la table de sinus est tirée des 3 bits suivant les 2 bits de poids fort de la phase. Elle effectue la séquence 0, 1, 2, 3, 4, 5, 6, 7, 0, 7, 6, 5, 4, 3, 2, 1, 0, 1, 2, 3, ....
La table de sinus contient les valeurs hexadécimales 0000 ou 7FFF (selon la valeur du deuxième bit de poids fort), 0000, 18F9, 30FB, 471C, 5A82, 6A6D, 7641 et 7D89.
Lorsque le bit de poids fort de la phase vaut '1', la valeur lue de la table change de signe pour donner la sortie.
Simulation
Interpolation
L'interpolation se fait en associant une fonction polynomiale d'ordre 3 entre chaque point de la table de sinus:
y = a·k3 + b·k2 + c·k +d
Au cours du calcul, le point courant de la table de sinus est défini en k = 0, le point précédent en k = -1 et le point suivant en k = 1. Nous calculerons la valeur du polynome pour n = 2m points situés entre 0 et 1.
Pour assurer la continuité entre le polynôme qui relie le segment -1 < k < 0 et celui qui relie 0 < k < 1, nous spécifons la dérivée au point y(k=0) comme étant égale à la pente entre les points y(k=-1) et y(k=1). Nous ferons de même pour tous les points de la fonction à interpoler.
Le segment 0 < k < 1 est donc soumis aux 4 conditions suivantes
y(k=0) = y0: le polynôme passe par le point (k=0, y=y0),
y(k=1) = y1: le polynôme passe par le point (k=1, y=y1),
y'(k=0) = [y(k=1) - y(k=-1)] / 2: la dérivée au point (k=0) est la pente entre y(k=-1) et y(k=1),
y'(k=1) = [y(k=2) - y(k=0)] / 2: la dérivée au point (k=1) est la pente entre y(k=0) et y(k=2).
Ces 4 conditions nous servent à déterminer les 4 coefficients a, b, c et d du ploynôme à partir des 4 points y(k=-1) à y(k=2) de la courbe à interpoler. La résolution de ce système d'équations nous donne les valeurs suivantes des coefficients:
a = 1/2 [ - y(k=-1) +3·y(k=0) -3·y(k=1) + y(k=2) ]
b = 1/2 [ 2·y(k=-1) -5·y(k=0) +4·y(k=1) - y(k=2) ]
c = 1/2 [ - y(k=-1) + y(k=1) ]
d = y(k=0)
Par souci de simplification, nous calculerons le double de la valeur des coefficients et par la suite nous diviserons la valeur du polynome calculé par 2.
A chaque nouvelle valeur du signal d'origine (ici, de la table de sinus), il faut recalculer les coefficients du polynôme. Puis, à chaque période d'horloge et en attendant l'arrivée de la valeur suivante, on calcule la fonction polynomiale pour déterminer la valeur courante de l'échantillon de sortie.
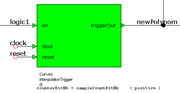
Générateur d'impulsions de séquencement
Ce circuit fournit une impulsion qui dure une période d'horloge à chaque changement de polynôme, c'est-à-dire pour chaque nouveau segment de courbe.
Ceci se fait chaque 2n périodes d'horloge où en = '1', avec n = sampleCountBitNb = phaseBitNb-2-tableAddressBitNb. Dans notre exemple de laboratoire, phaseBitNb = 10 et sampleCountBitNb = 5.
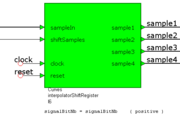
Registre à décalage
A chaque impulsion de synchronisation shiftSamples, le circuit mémorise le nouvel échantillon de la fonction à interpoler, sampleIn, et le mémorise comme dernière valeur d'échantillon, sample4. En même temps, il décale l'échantillon sample4 dans sample3, etc...
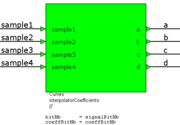
Calcul des coefficients
Les coefficients se calculent comme suit:
a = - sample1 +3·sample2 -3·sample3 + sample4
b = 2·sample1 -5·sample2 +4·sample3 - sample4
c = - sample1 + sample3
d = sample2
Vos coefficients peuvent être vérifiées par le chronogramme ci-contre.
Calcul du polynôme
Le polynôme se calcule de manière itérative.
Ainsi, pour une fonction de premier ordre, y(x) = a·x + b, la valeur suivante vaut y(x+eps) = y(x) + a·eps. Ceci se calcule en initialisant u = a·eps, y(0) = b, et en calculant y(i+1) = y(i) + u à chaque nouvelle période d'horloge.
Pour une fonction de deuxième ordre, y(x) = a·x2 + b·x + c, ce qui donne y(x+eps) = y(x) + u(x), avec u(x) = 2·a·eps·x + (a·eps2 + b·eps). L'incrément u(x) se calcule de la manière définie pour une fonction du premier ordre. Ceci se calcule donc en initialisant v = 2·a·eps2, u(0) = a·eps2 + b·eps,y(0) = c et en calculant y(i+1) = y(i) + u(i) et u(i+1) = u(i) + v à chaque nouvelle période d'horloge.
Le calcul de la fonction de troisième ordre se fait de manière similaire.
Pour le calcul numérique, eps est choisi comme égal à une puissance négative de 2, ce qui permet de la calculer par un décalage. De même, pour rester avec des nombres entiers, on calculera la fonction y(i) multipliée par une puissance de 2 et un décalage terminal nous donnera la valeur finale des échantillons du polynôme.
Notre algorithme est donc le suivant:
- A l'arrivée d'un nouvel échantillon, il faut calculer les valeurs initiales utilisée pour développer le polynôme de manière itérative.
- Entre deux échantillons d'entrée, le calcul de la fonction polynomiale se fait par additions à l'aide des équations itératives.
Les valeurs initiales sont les suivantes:
x = 2·d·2(3·m)
u = a + b·2m + c·2(2·m)
v = 6·a + 2·b·2m
w = 6·a
y = d
Le calcul itératif du polynôme se fait comme suit:
x = x + u
u = u + v
v = v + w
y = x / (2·2(3·m))
Il est évident que, du fait des décalages 2m, le nombre de bits des signaux internes devra être plus élevé que le nombre de bits des échantillons d'entrée ou de sortie. En fonction de la valeur du décalage m = oversamplingBitNb, estimer la taille nécessaire pour ces signaux. Les déclarer avec 8 bits supplémentaires pour s'assurer de ne pas avoir de dépassement de capacité.
A nouveau, la fonction resize sera très utile ici.
Simulation
Navigation
![]() 01 Generateur
01 Generateur
![]() Travaux de laboratoire
03 Convertisseur numérique / analogique
Travaux de laboratoire
03 Convertisseur numérique / analogique ![]()